摘要
- 识别和应用机器学习算法解决问题
- 机器学习算法备忘单
- 何时使用特定算法? 线性回归 vs 逻辑回归,Linear SVM vs kernel SVM,Trees
- 神经网络和深度学习:k-means/k-modes,GMM,Hierarchical clustering,PCA,SVD,LDA
Machine Learning Algorithms Overview
关于目前最流行的一些机器学习算法,建议阅读:
如果您已经非常熟悉这些算法,可以跳过本节。
Which machine learning algorithm should I use?
面对各种机器学习算法时,经常遇到的一个典型问题是“我应该使用哪种算法?” 问题的答案取决于许多因素,其中包括:
- 数据的大小,质量和性质
- 可用的计算时间
- 任务的紧迫性
- 你想对数据做什么
即使是一位经验丰富的数据科学家,也无法在尝试不同的算法之前知道哪种算法会表现最好。我们并不主张这是唯一的、完美的方案,而是希望能够根据一些明确的因素提供指导——首先应该尝试哪些算法。
机器学习算法备忘单
机器学习算法备忘单(The machine learning algorithm cheat sheet)可以帮助您从各种机器学习算法中进行选择,以找到适合您的特定问题的适当算法。本文将说明使用备忘单的过程。
由于备忘单是为初学者数据科学家和分析师设计的,因此在讨论算法时会做一些简化假设。这里推荐的算法来自几位数据科学家和机器学习专家和开发人员的反馈和提示。有几个问题我们的看法并不一致,对于这些问题,我们试图强调通用性、尽量调和差异。随着我们的知识库发展,将包含一套更完整的方法,其他算法将在稍后添加。
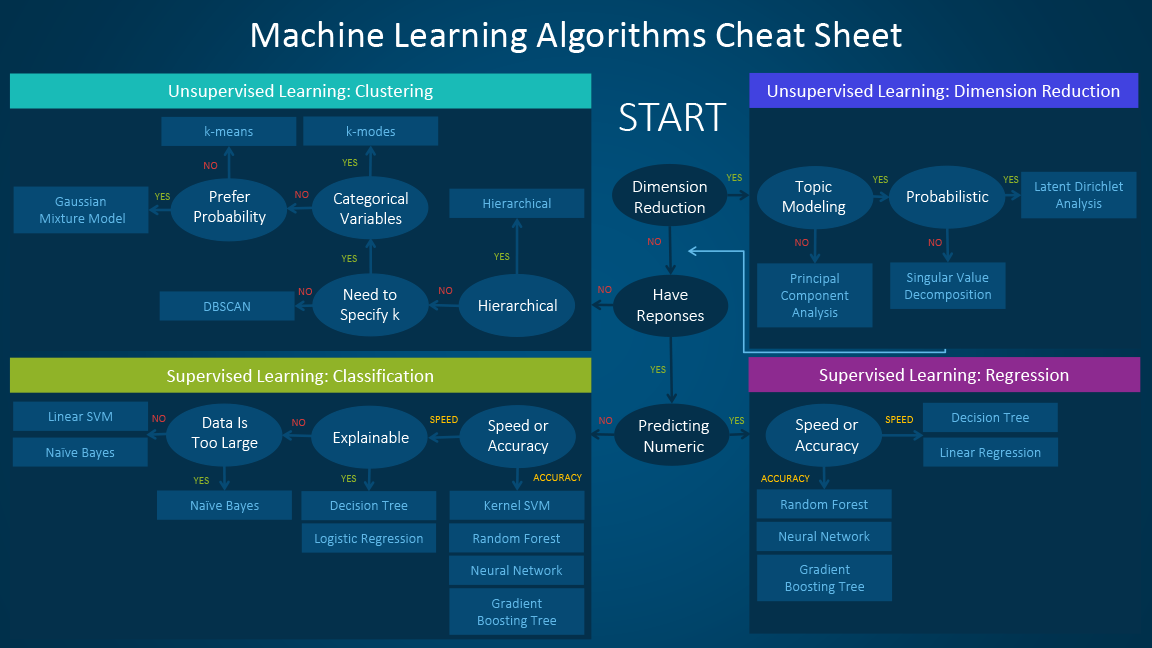
如何使用备忘单
备忘单使用方法,依次阅读的路径和算法标签,例如:
- 如果要执行降维(dimension reduction),则使用主成分分析(principal component analysis)
- 如果您需要快速进行数值预测(numeric prediction),请使用决策树(decision tree)或逻辑回归( logistic regression)
- 如果您需要分层结果,则使用分层聚类(hierarchical clustering)
有些场景可能会适用不止一个分支,也有些场景不能完美匹配上,重要的是要记住,这些路径只是基于经验的方法,因此一些建议并不完全准确。许多数据科学家的关电视,找到最好算法的唯一方法就是尝试所有算法(the only sure way to find the very best algorithm is to try all of them)。
何时使用特定算法?
线性回归 vs 逻辑回归
线性回归是一种讨论连续因变量之间关系的建模方法。如果因变量不是连续的而是分类的,则可以使用 logit link function 将线性回归转化为逻辑回归。逻辑回归是一种简单,快速而强大的分类算法。这里我们讨论二进制情况下的因变量
在逻辑回归中,我们使用不同的假设类来尝试预测给定示例属于“1”类的概率与其属于“-1”类的概率。
| 线性回归 | 逻辑回归 |
|---|---|
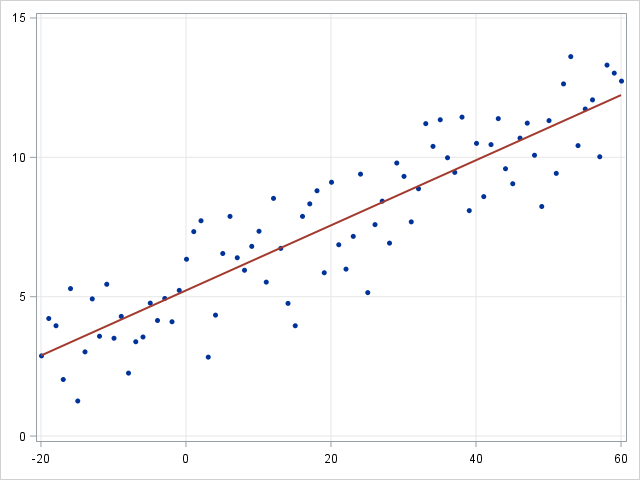 |
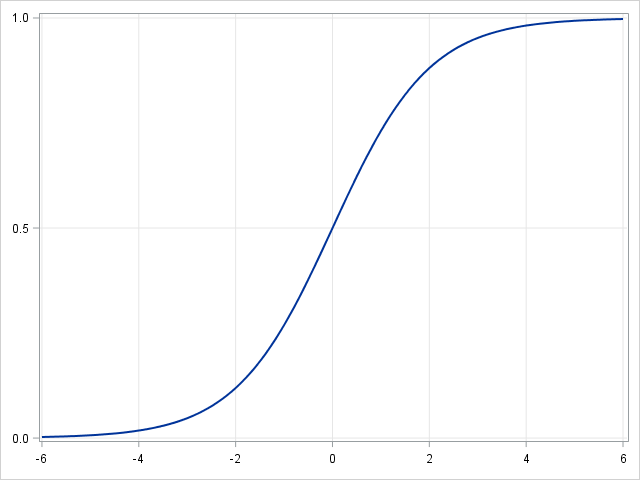 |
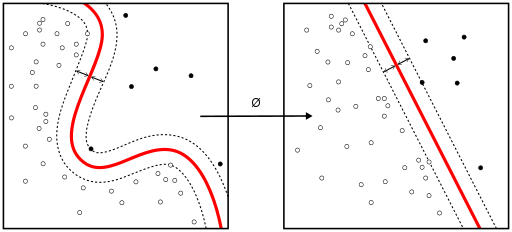
Linear SVM vs kernel SVM
当数据的各种类型不是线性可分的时候,核方法(Kernel method 或 Kernel tricks)可以用来将非线性可分的空间映射到更高维的线性可分的空间。
支持向量机(SVM)算法相当于通过法线(Normal vector)和超平面偏差(bias of the hyperplane)获得分类器。这个超平面(边界)尽可能宽地分隔不同的类,该问题可以转化为约束优化问题。
当大多数因变量是数字时,逻辑回归和 SVM 是首先应该尝试的分类方法。这些模型易于实现,参数易调整,性能也相当不错。非常适合初学者。
| 线性回归 | 逻辑回归 |
|---|---|
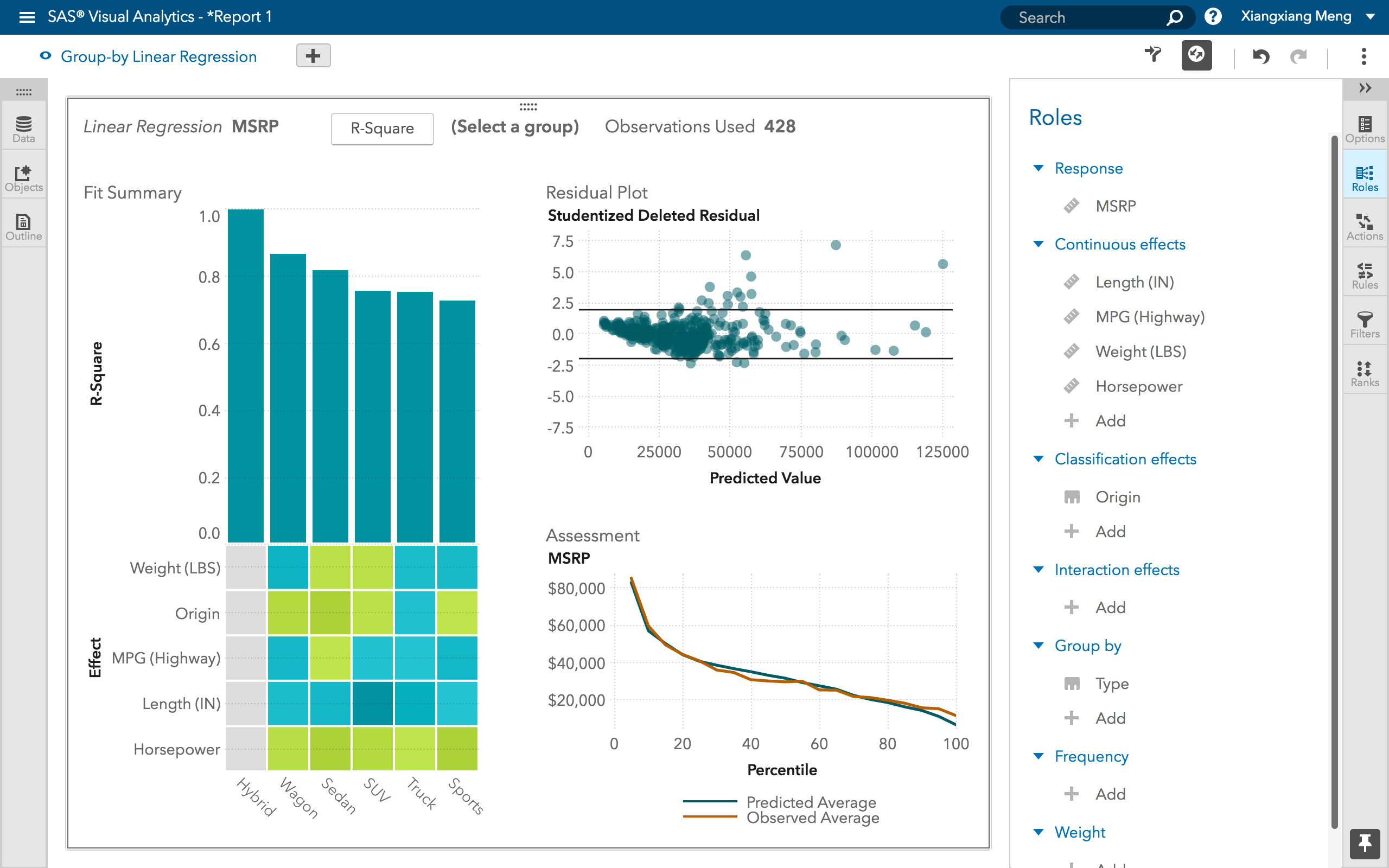 |
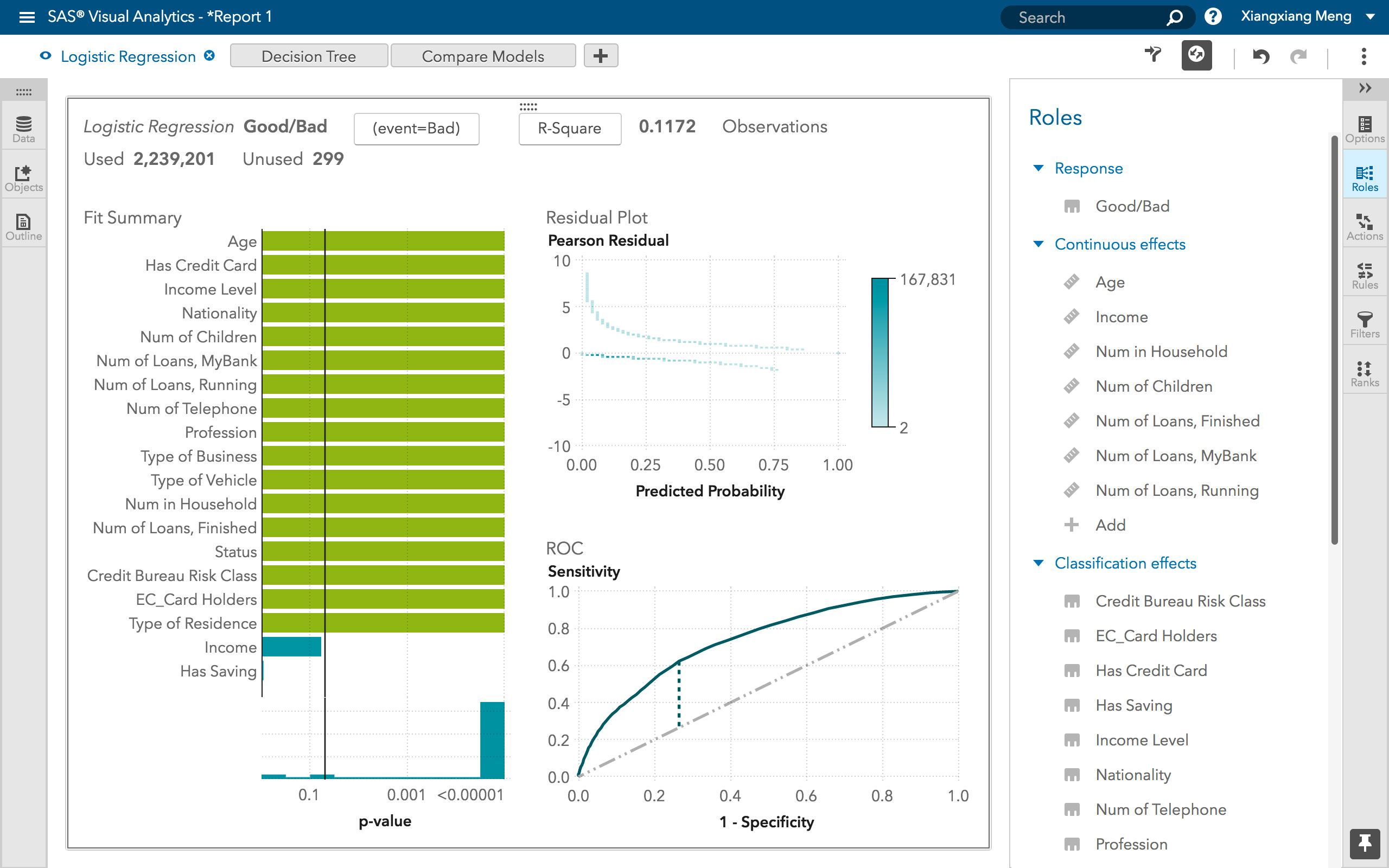 |
树 | Tree
- 预测模型中的决策树
决策树(Decision Tree),随机森林(Random Forest)和梯度提升(Gradient Boosting )都是基于决策树的算法。决策树有许多变体,但它们都做同样的事情 - 将特征空间细分成大多数标签相同的区域。决策树很容易理解和实施。但是,当我们耗尽树枝(branch)并且深入时,它们倾向于过度拟合数据。随机森林和梯度提升是两种使用树算法的实现,具有良好的精确度,是克服过拟合问题(over-fitting problem)的流行方法。
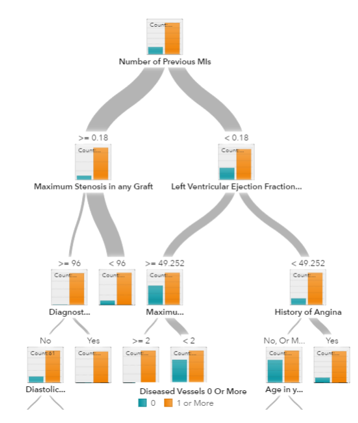
注:在统计学中,过拟合(overfitting,或称过度拟合)现象是指在拟合一个统计模型时,使用过多参数。对比于可获取的数据总量来说,一个荒谬的模型只要足够复杂,是可以完美地适应数据。过拟合一般可以视为违反奥卡姆剃刀原则。当可选择的参数的自由度超过数据所包含信息内容时,这会导致最后(拟合后)模型使用任意的参数,这会减少或破坏模型一般化的能力(目标效果应适用于一般化的情况而非只是训练时所使用的现有数据(根据它的归纳偏向))。另一种常见的现象是使用太少参数,以致于不适应数据,这则称为乏适(underfitting,或称:拟合不足)现象。
神经网络和深度学习
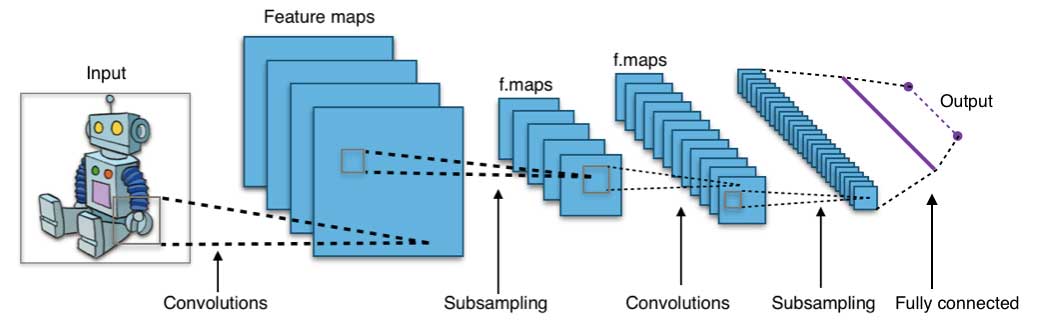
神经网络在 20 世纪 80 年代中期由于其并行和分布式处理能力而兴旺发达。但是在这个领域的研究受反向传播算法无效性的阻碍,它广泛用于优化神经网络参数。支持向量机(SVM)和其他更简单的模型,可以通过求解凸优化问题来轻松训练,逐渐取代机器学习中的神经网络。
近年来,诸如无监督预训练( unsupervised pre-training)和分层贪婪训练(layer-wise greedy training)等新的和改进的训练技术促进了神经网络的复兴。日益强大的计算能力,例如图形处理单元(GPU)和大规模并行处理(MPP),也刺激了神经网络的发展,已经发明出具有数千层的神经网络模型。
注:反向传播(Backpropagation,缩写 BP)是“误差反向传播”的简称,一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
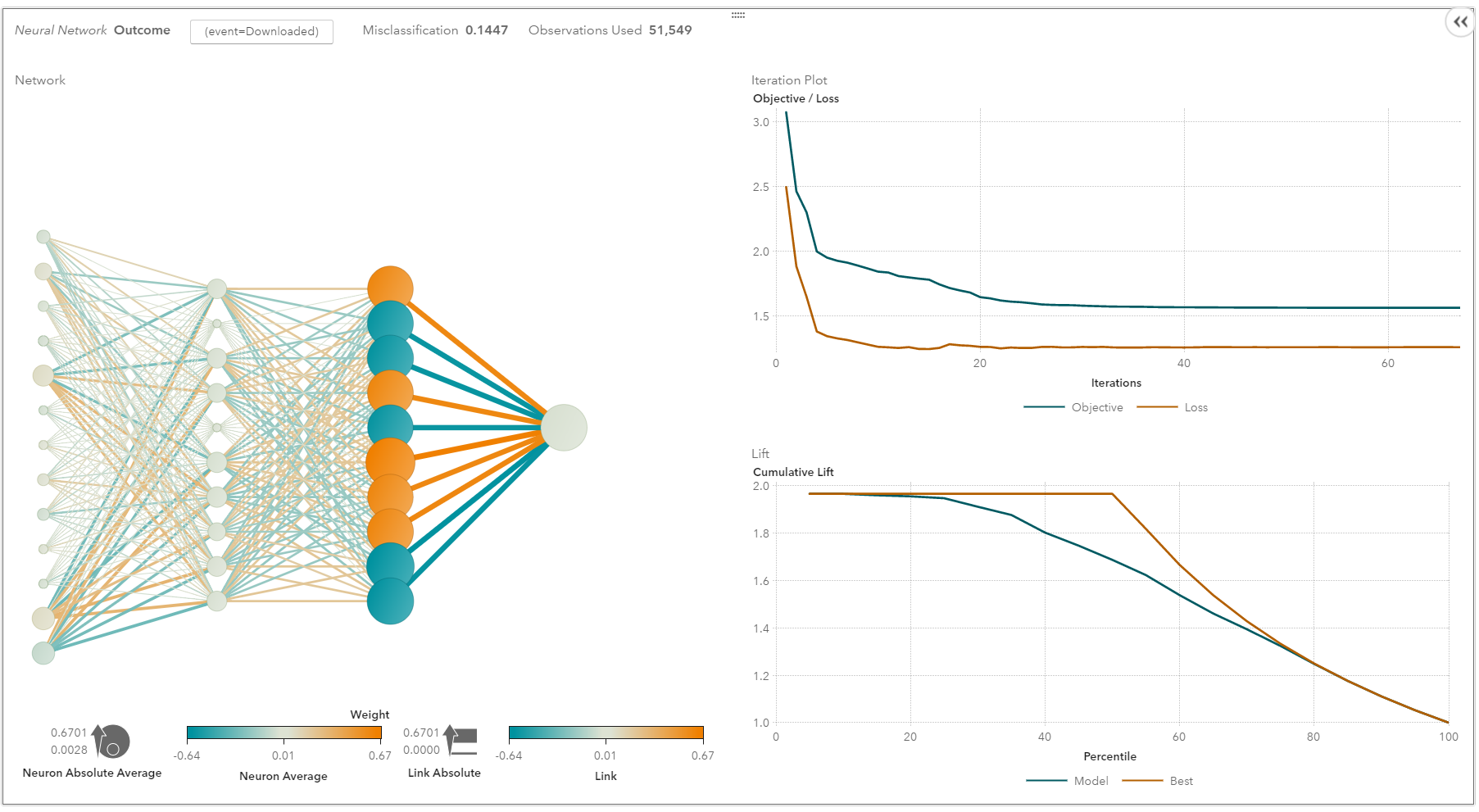
SAS Visual Analytics 中的神经网络
换句话说,浅层神经网络已演变成深度学习神经网络。深度神经网络对于监督学习非常成功。当用于语音和图像识别时,深度学习的表现与人类一样好,甚至更好。应用于无监督学习任务(如特征提取),深度学习还可从原始图像或语音中提取特征,而人工干预则更少。
神经网络由三部分组成:输入层(input layer),隐藏层(hidden layers)和输出层(output layer)。训练样本定义了输入层和输出层。当输出层是一个分类变量时,神经网络就是解决分类问题的一种方法。当输出层是连续变量时,网络可以用来做回归。当输出层与输入层相同时,网络可用于提取内在特征。隐藏层的数量决定了模型的复杂性和建模容量。
k-means / k-modes,GMM(高斯混合模型)聚类
k-means / k-modes,GMM 聚类旨在将 n 个观测分为 k 个聚类。 简单地说,k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了,即 hard assignment,而 GMM 则给出这些数据点被 assign 到每个cluster 的概率,又称作 soft assignment 。每个样本都有与每个群集关联的概率。当给定聚类数 k 时,两种算法都足够简单快速地进行聚类。
| k-means | GMM |
|---|---|
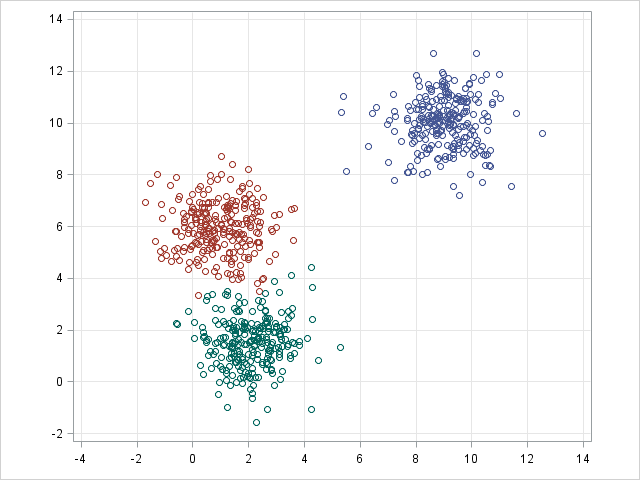 |
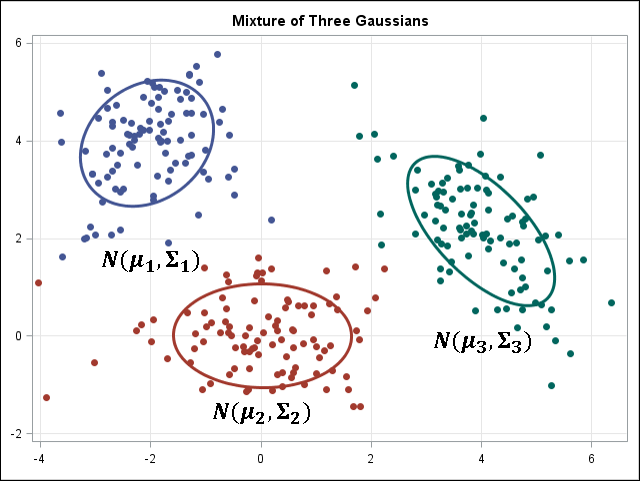 |
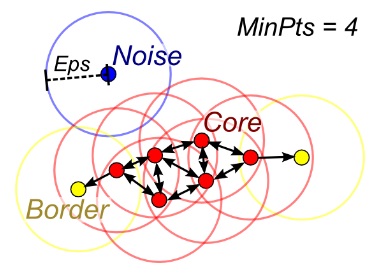
DBSCAN | 基于密度的空间聚类
DBSCAN ,Density-based spatial clustering of applications with noise ,是在 1996 年由 Martin Ester 等提出的聚类分析算法, 这个算法是以密度为本的:给定某空间里的一个点集合,该算法能把附近的点分成一组(有很多相邻点的点),并标记出位于低密度区域的局外点(最接近它的点也十分远),DBSCAN 是一个最常用的聚类分析算法。
Hierarchical clustering | 分层聚类
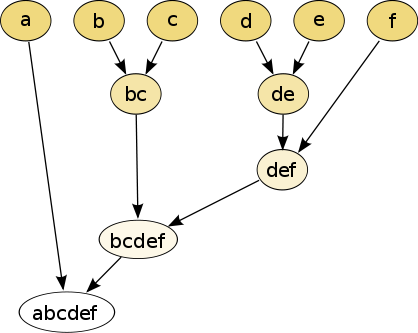
分层分区可以使用树结构(树状图)可视化。它不需要集群的数量作为输入,并且可以使用不同的 K 来在不同粒度级别处查看分区(即精炼/粗化集群 refine/coarsen clusters)。
PCA,SVD和LDA
我们通常不希望直接将大量特征提供给机器学习算法,因为某些特征可能无关紧要,或者“内在”维度可能小于特征的数量。主成分分析(PCA,Principal components analysis),奇异值分解(SVD,Singular value decomposition)和隐含狄利克雷分布(LDA,latent Dirichlet allocation)均可用于降维。
PCA 是一种无监督聚类方法,它将原始数据空间映射到较低维空间,同时保留尽可能多的信息。 PCA 基本上找到最能保留数据方差的子空间,子空间由数据协方差矩阵的主要特征向量定义。
SVD 和 PCA 有一定联系——中心数据矩阵的 SVD(特征 vs. 样本)能提供定义由 PCA 所找到的同样子空间的主左奇异向量(dominant left singular vectors)。然而,SVD 是一种更通用的技术,因为它也可以做 PCA 不能做的事情。例如,用户与电影矩阵的 SVD 能够提取可以在推荐系统中使用的用户资料和电影资料。另外,在自然语言处理(NLP)中,SVD 还被广泛用作主题建模工具,称为潜在语义分析( latent semantic analysis )。
NLP 中的相关技术是隐含狄利克雷分布( LDA )。 LDA 是概率性主题模型,它以与高斯混合模型(GMM)相似的方式,即将连续数据按照高斯密度分解——将文档分解为主题。与 GMM 不同的是,LDA 对离散数据(文档中的词)进行建模,并且它约束了主题需是根据狄利克雷分布的先验分布。
总结:选择算法时的注意事项
选择算法时请始终考虑以下方面:准确性(accuracy),训练时间(training time)和易用性(ease of use)。许多用户将准确性放在首位,而 初学者倾向于关注他们最熟悉的算法(Beginners tend to focus on algorithms they know best)。
首先要考虑的是如何获得结果,无论结果如何。初学者倾向于选择易于实现并能够快速获得结果的算法(Beginners tend to choose algorithms that are easy to implement and can obtain results quickly)。这个工作无可厚非,只需确保它只是整个过程的第一步。一旦您获得了一些结果并熟悉数据,您可能需要花更多时间、使用更复杂的算法来加强对数据的理解,从而进一步改进结果。
最好的算法也许不是那些已经获得最高准确率的方法,因为算法通常需要仔细调整、广泛训练才可以实现可用性方面的最佳性能。
扩展阅读
《The Machine Learning Master》

- Machine Learning(一):基于 TensorFlow 实现宠物血统智能识别
- Machine Learning(二):宠物智能识别之 Using OpenCV with Node.js
- Machine Learning:机器学习项目
- Machine Learning:机器学习算法
- Machine Learning:如何选择机器学习算法
- Machine Learning:神经网络基础
- Machine Learning:机器学习书单
- Machine Learning:人工智能媒体报道集
- Machine Learning:机器学习技术与知识产权法
- Machine Learning:经济学家谈人工智能
- 数据可视化(三)基于 Graphviz 实现程序化绘图
参考文献
- Which machine learning algorithm should I use? | Hui Li | Principal Staff Scientist, Data Science
- An Information-Theoretic Analysis of Hard and Soft Assignment Methods for Clustering
- Greedy Layer-Wise Training of Deep Networks
- Understanding and interpreting your data set 1
- KERNEL METHODS IN MACHINE LEARNING1 |By Thomas Hofmann, Bernhard Scholkopf and Alexander J. Smola

